一、教学价值分析
1.圆锥曲线中动直线过定点问题是对圆锥曲线性质的进一步应用，综合了直线、圆锥曲线、向量等基础知识，包含了分类讨论、数形结合思想，函数与方程思想、转化与化归等多种数学思想，考察学生的综合能力；
2.符合考试大纲中“对数学能力的考查要以数学基础知识、数学思想和方法为基础”的要求，是高考的重要考点.
二、教学内容分析
技能：条件转化，多元表征.
思维方法：转化与化归思想、数形结合思想、方程思想、分类讨论.
三、教学任务分析
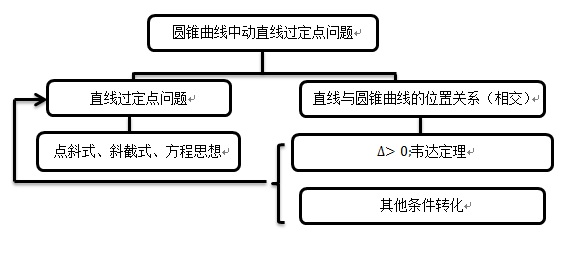
四、学习者分析
圆锥曲线中动直线过定点问题，是直线的方程与圆锥曲线这两部分知识的综合考察，综合了多种数学思想，且计算量大.学生已掌握直线过定点问题，以及直线与圆锥曲线的位置关系，但学生在条件转化及计算能力方面还有待提高.
五、目标的精确描述
1.通过联立直线与圆锥曲线方程，判断
，利用韦达定理，找出两交点横坐标之间的关系；
2.能将题目中的条件转化为与结论有关的等量关系（多元表征）；
3.体验解析几何中的计算过程.
六、作业与评估设计
七、教学过程整体设计
启动 动直线过定点，直线与圆锥曲线的位置关系的判断.
建构 圆锥曲线中动直线过定点问题解题思路.
巩固 在平面直角坐标系xOy中，直线l与抛物线y2＝4x相交于不同的A、B两点.如果·＝－4，证明直线l必过一定点，并求出该定点.
总结 圆锥曲线中动直线过定点问题思路总结及注意事项.
八、知识点的微设计
（一）建构：圆锥曲线中动直线过定点问题解题思路.
2、条件2“以AB为直径的圆过椭圆C的右顶点P”可以转变为怎样的等量关系？
（二）总结：圆锥曲线中动直线过定点问题解题思路：
（三）巩固
1.在平面直角坐标系xOy中，直线l与抛物线y2＝4x相交于不同的A、B两点.如果·＝－4，证明直线l必过一定点，并求出该定点.
九、成品输出
教学设计、课件、学案、课后作业
