五星网状教学模式数学教案

一、教学价值分析

通过本节课的学习，加强学生的推理论证能力和运算求解能力，升华数形结合和转化与化归的数学思想，提升学生逻辑推理和数学运算学科核心素养。

二、教学内容分析

1、原理：直线和抛物线的位置关系

2、运用：焦点弦长，最值、范围问题，定点、定值问题

3、思维方法：数形结合、转化与化归。

三、教学任务分析

上位知识：直线的方程、抛物线的方程及定义、弦长公式、一元二次方程的根等。

同位知识：韦达定理等；

支撑知识：1、曲线交点的求法，二次方程根的个数的判断；

2、直线与抛物线的方程及定义，韦达定理，基本不等式；

3、数学中最值问题的常见求法。

四、学习者分析

1、学生初中已经学习了二次方程根的个数的判定；

2、学生也掌握了直线和抛物线的定义及方程。

3、学生对于数学中最值问题的常见求法有一定了解。

4、直线与椭圆的位置关系的判定方法已掌握。

5、这是高三复习课，学生在高二时已学习过相关内容。

五、学习目标精准描述

1、会判定直线与抛物线的位置关系，并会熟练运用它们解决焦点弦长、最值与范围、定点与定值等相关问题。

2、通过本节课的学习，加强推理论证能力和运算求解能力，提升逻辑推理和数据分析学科核心素养。

3、通过本节课的学习，体验数学的逻辑性和严密性，感受数学之美

六、知识点微设计

知识点建构一：直线与抛物线的位置关系

【启动】

例1：已知直线l：y＝kx＋1，抛物线C：y²＝4x，当k为何值时，l与C有一个公共点。

变式：（1）当k为何值时，l与C有两个公共点； （2）当k为何值时，l与C没有公共点．

小结：

如何判定直线与抛物线的位置关系？

【巩固】

1. 抛物线y＝－x²上的点到直线4x＋3y－8＝0距离的最小值是________

2.已知顶点在原点，焦点在y轴上的抛物线被直线x－2y－1＝0截得的弦长为，求此抛物线方程．

知识点建构二：最值、范围问题

【建构】

考点二：最值、范围问题

例2：（2017、全国1卷理数、10）已知F为抛物线C：y²=4x的焦点，过F作两条互相垂直

的直线l₁，l₂，直线l₁与C交于A、B两点，直线l₂与C交于D、E两点，则|AB|+|DE|的最

小值为_____________

【总结】

1. 焦半径或焦点弦相关的最值问题，通常如何处理？

2.若AB是抛物线的焦点弦（过焦点的弦），且，，则

3.若AB是抛物线的焦点弦（过焦点的弦），则________

【运用】

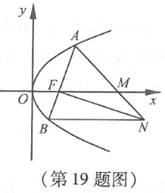
【总结】

1.直线与圆锥曲线的综合性问题中，一般如何解决范围或最值问题？

2.直线和圆锥曲线的综合性问题通常考查什么数学思想方法和核心素养？

3.如何判定直线和圆的位置关系？

4.数学运算中，有哪些常见的技巧和方法？

七、课堂评估与课后作业设计

课后作业

八、教学过程整体设计

知识点建构一：直线和抛物线位置关系的判定及运用

启动：

建构：直线与抛物线的位置关系：

运用：

巩固

知识点建构二：最值、范围问题

启动：

建构：最值、范围问题的求解思路和方法

巩固：

课后练习

知识总结：（问自己是否记住）

能力总结：（问自己能否做到）

九、成品

学案